Hello,
In this thread, I want to introduce a LIP addressing the roadmap objective “Incentivise standby delegates”. The proposal introduces three main improvements:
- A source of randomness on the blockchain,
- Two new block forgers every round, those will be chosen randomly from the standby delegates,
- Using this new source of randomness to order the forging delegates.
I’m looking forward to your feedback.
Here is a complete LIP draft for the solution:
LIP: lip-ikeralustiza-use_randao-based_scheme_to_include_standby_delegates_and_reorder_delegate_list
Title: Use Randao-based scheme to include standby delegates and reorder delegate list
Author: Iker Alustiza <iker@lightcurve.io>
Discussions-To:
Type: Standards Track
Created: <YYYY-MM-DD>
Updated: <YYYY-MM-DD>
Abstract
This LIP proposes to include two standby delegates in the forging delegate list of every round to incentivize a greater number of online nodes in the Lisk network. The selection of these standby delegates is done by a Randao-based weighted random selection scheme to ensure the fairness and unpredictability of the process. This scheme is also used to reorder the forging delegates list in every round.
Copyright
This LIP is licensed under the Creative Commons Zero 1.0 Universal.
Motivation
Since the Bitcoin network was released back in 2009, the number of online nodes has been an important figure to assess the health and decentralization of a certain blockchain. In general, nodes can be thought as the backbone of a blockchain, they contribute to keep the network decentralized and protect the protocol’s consensus rules. This is done by validating every new transaction and block and eventually broadcasting them, and, usually, by keeping a complete copy of the blockchain. Hence the more online nodes a network has, the more secure and decentralized it is. However, in the majority of the existing blockchains, most of the online nodes do not get a direct reward for this work, and only those nodes that actively participate in the block production (e.g., miners in Bitcoin or active delegates in Lisk) get a block reward. At first sight, this may look like a misalignment of network incentives. One could argue that there are enough incentives to run a node, but the experience shows that nodes are run mainly because there is an expected profit in doing so. This profit can be generated by getting network rewards (e.g., generating new blocks), or by providing a service to customers (e.g., cryptocurrency exchanges). This situation is also present in Lisk where only the active delegates (top 101 by rank) get a reward and collect the transaction fees for forging new blocks. In the same way as in Bitcoin, the rest of online nodes, which also broadcast and validate blocks and transactions, do not get anything in exchange. Also, in the Lisk DPoS system there are the so-called standby delegates, which are all the delegates below the rank 101 in the delegate list (1688 at the time of writing this document). As it is the case with the rest of the nodes that are not run by delegates, online nodes run by standby delegates get no reward from being part of the network even though they may have a considerable delegate weight (i.e., a considerable amount of LSK tokens voting for them). This proposal aims to change this by allowing these standby delegates to participate in the block forging with a probability proportional to their delegate weight. This will create an incentive for these delegates to run Lisk nodes, and an incentive for some LSK holders to register new delegates. And consequently, this should facilitate the achievement of the original objective of a more secure, decentralized and stable network for Lisk.
Rationale
This LIP proposes to include 2 standby delegates in the forging delegate list every round with a probability proportional to their delegate weight. This implies that the rounds are now constituted of 103 block slots where 101 active delegates and 2 standby delegates are randomly assigned to each of these slots. The selection of these standby delegates is done by a low-complexity randomized selection algorithm. To ensure the fairness and unpredictability of the output of the process, the random seed of this algorithm is generated by a commit-reveal procedure based on the Randao scheme proposed for blockchains adapted to Lisk. Also, given the properties of the generated random seed, this LIP proposes to use it as the input seed to reorder the forging delegates list.
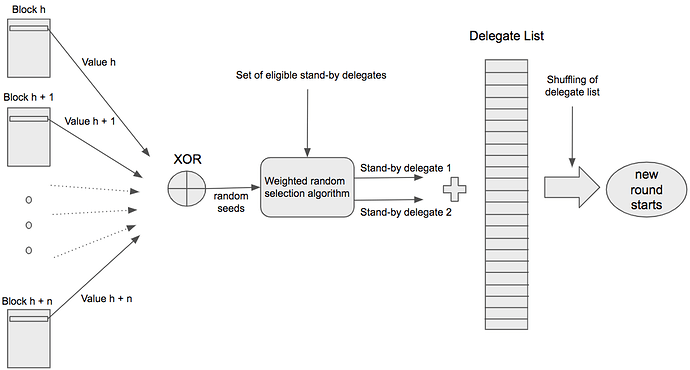
In the following subsections, the key points and changes of this proposal are justified and explained in detail. However, for a quick overview, the diagram below provides a very high level description of what this proposal entails:
Random Seed Generation
The demand of randomness for decentralized applications and, in special, for blockchain technology has increased notably in the last years. For example, a secure Proof of Stake system requires a source of randomness to select the next block generator. However, the problem of generating a good random seed has proven to be a very challenging issue for these applications. Conventional number generators (based on a physical input or a computational algorithm) are not suitable since they imply a trusted setup. Here the random seed generation process has to be decentralized in the way that a single output is computed from the input of multiple independent parties. In this context, a good random seed is a random seed with the following properties:
- Unpredictable: No one can predict the value of the next random seed based on past information.
- Unbiasable: None of the parties involved in the seed generation can bias the output of the process.
- Conspiracy-resistant: As long as there are honest participants, collusion of some of the participating parties cannot bias the outcome.
- Available (liveness): As long as there are honest parties involved in the seed generation, a random seed can be computed.
- Tamper-resistant: No-one can modify the output of the random seed generation process once the process is completed.
- Verifiable: Everyone can verify that the output is correct once the random seed generation process is completed.
- Unconcealable: The parties involved in the seed generation cannot refuse to disclose the output of the process.
The theoretical problem of generating a random seed that fulfils each of these properties is still an open problem and a considerable effort is currently being spent on it (an example of this is the work on Verifiable Delay Functions by Justin Drake et al. for Ethereum 2.0). With this consideration, in this proposal a random seed generation scheme is presented which generates a good enough random seed under the assumption that at least one honest delegate participated in the seed generation process. This random seed is good enough in the way that even though it is not unpredictable or unbiasable by definition, the new incentives created in the protocol make biasing or predicting the seed not profitable for the attacker. This scheme is described in detail in the next subsection.
Randao-based scheme with hash onion adapted to Lisk
The approach proposed here is based on a Randao-like scheme with a hash onion for the commit-reveal process to generate the random seed for the next round. Particularly, the proposed scheme follows the next steps:
-
Every delegate computes locally a hash onion, H(H(H(… S…))), where S is any arbitrary number chosen by the delegate and with an arbitrarily large number of hash layers. H is a cryptographic hash function with 128 bits output.
-
Every forging delegate adds a 128 bit value, Ch, at heigh h to its forged block. If a delegate forges at heights h1, h2,…, in one chain, then the values should satisfy H(Chi ) = Chi-1 for every i > 1, i.e., the delegate iteratively reveals the preimage (the next inner layer of the hash onion) of the value committed in its previously forged block.
-
Assuming that every round contains n blocks and the current round r started at block height h, then two random seeds, rs1 and rs2, are computed in the following way:
-
rs1 = XOR ( H (h + ⌊n/2⌋), Vh - ⌊n/2⌋, Vh - ⌊n/2⌋ + 1, …, Vh + ⌊n/2⌋ )
-
rs2 = XOR ( H (h -1), Vh - n, Vh - n + 1, …, Vh - 1 )
where every Vk in ( Vh - n, Vh - n + 1, …, Vh + ⌊n/2⌋) is assigned as Vk = Ck if the delegate forging at height k previously forged at height k’ with H(Ck) = Ck’, i.e., the delegate correctly revealed the committed value, and Vk = 0 otherwise. This means that only correctly revealed values are considered in the random seed computation. Otherwise the revealed values are not taken into account for the random seed.
-
Then rs2 is used as a random seed for the randomized algorithm to select one standby delegate whereas rs1 is used as a random seed to select the other standby delegate and to re-order the delegate list for round r + 1. This requires that at least one honest delegate participates in the computation of each of the seeds rs1 and rs2.
It is worth mentioning that in general H( ) can be any cryptographic hash function. For simplicity and to save space in the block header, in this proposal H( ) is constructed by truncating the SHA-256 output to the 128 most significant bits.
Mitigating last revealer attack and incentives
It is known that commit and reveal based schemes like Randao can be slightly biased by the last revealer attack. A last revealer attack occurs when the last member to reveal its value, in this case the delegate forging at height h + ⌊n/2⌋ (assuming that the current round r started at block height h), decides whether to reveal or not the correct value based on the effect on the final output, creating bias. Because this delegate may arbitrarily decide not to reveal a preimage of its previously committed value, the proposed scheme includes the following mechanisms that make this behaviour not profitable:
- If any forging delegate reveals a wrong value, i.e., H(Chi ) ≠ Chi-1, then the reward of the forged block is 0 (see Specification section for the details).
- Instead of a unique random seed output at the end of r, two random seeds, rs1 and rs2, are generated from partially independent revealed values. This implies that delegates forging at height h - 1 or at h + ⌊n/2⌋ could perform the last revealer attack, but also, this effectively reduces the effect of the bias to the selection of only one standby delegate per random seed.
- The delegate weights at the end of round r - 2 are considered1 to choose the standby delegates so that the delegate forging at height h + ⌊n/2⌋ cannot affect to its advantage the set of eligible standby delegates by submitting a vote transaction in the last block of r.
Thus delegates forging at heights h - 1 or at h + ⌊n/2⌋ can only choose to reveal a wrong value to bias the selection of one of the next round’s standby delegate forgers, but consequently, losing their forged block reward. This means that even in the best case scenario for the attackers, their expected profit is zero compared to revealing the correct value, i.e., there is no practical advantage for last revealers. What is more, the chances of having this best case scenario for the attacker are very low.
Set of Eligible Standby Delegates
It is also important to clearly define what are the parameters for a delegate to be part of the set of eligible standby delegates. In order to have a straightforward requirement, this proposal sets a minimum delegate weight as threshold to become an eligible standby delegate. This way, a delegate that has a delegate weight over or equal to this quantity is automatically eligible to forge a block and should run a Lisk node.
The minimum required delegate weight to become eligible is 1000 LSK. This quantity sets a low barrier for medium sized accounts to get a reward for securing the network. At the moment, there are more than 5000 accounts with a balance equal or higher than 1000 LSK that could immediately register a delegate, vote for themselves and become an eligible standby delegate. In the Appendix A, a brief study of the expected number of blocks forged by these accounts is included.
Weighted Random Selection Algorithm
Assuming that a random seed is available, two delegates have to be randomly selected every new round from the set of standby delegates with a probability proportional to their delegate weight. In computer science, the problem of choosing two samples out of an input set according to their weight has been usually addressed as weighted random selection or weighted random sampling. It is a commonly present topic for many applications, especially in statistical computing, data science and video-games development. Several algorithms can be found in the literature optimized for different situations (large input sets, large number of selected samples, unknown size of the sets, etc). However, here both the input set (number of eligible standby delegates) and the selected samples (two standby delegates per round) are rather small. Thus the proposed algorithm aims for simplicity, robustness and performance for this specific case.
The high-level description of the algorithm is as follows:
- Generate an ordered list with the set of eligible standby delegates, Ssb. The list is ordered by delegate weight. Assuming the current round r, the list is generated with the account state information at the end of r - 2.
- Create a first number rnd1 = rs1 mod dwsb where dwsb is the sum of all the delegate weights in Ssb. rnd1 is approximately uniformly distributed in the interval [0, dwsb).
- Associate to every delegate in Ssb a part of the interval [0, dwsb) and select the first standby delegate D1 using rnd1.
- Create a second number rnd2 = rs2 mod dw’sb where dw’sb is the sum of all the delegate weights in Ssb after removing D1 from the list. rnd2 is approximately uniformly distributed in the interval [0, dw’sb).
- Associate to every delegate in Ssb, after removing D1, a part of the interval [0, dw’sb) and select the second standby delegate D2 using rnd2.
With this algorithm, and assuming that rs1 and rs2 are uniformly distributed, some standby delegates will have a probability 10-22 higher of being selected than others, which is more than acceptable for this case.
Specification
Block Header
This proposal requires to add an additional property, seedReveal, to the block header. seedReveal has to be a 128 bit value that contains the new value revealed by each forging delegate every round. Also, in a JSON object representing the block header, seedReveal has to be represented as a hexadecimal string.
This additional property needs to be included in the byte array that is used for generating the signature and blockID of a block. This way this property cannot be altered by a malicious node. For this, the getBytes() function needs to additionally include the 16 bytes of seedReveal value in big-endian encoding. It should be included in the byte array directly after the previousBlock property.
Hashing Function
As introduced in the previous section, a new hashing function, H(), is defined:
-
Input: A bit string of arbitrary length,
input. -
Output: A 128-bit string,
digest. -
Pseudo-code:
H(input): t = SHA-256(input) digest = trunc(t) return digestwhere the function
trunc()truncates its input to the 128 most significant bits.
Validating New Block Header Property
In order to implement the random seed generation scheme introduced in the previous section, new rules need to be in place for a new block B to be valid. Assume A is the last block forged by the forger of B on the same chain and in the previous round or in the same round of B. Then:
- If
B.seedRevealis a preimage ofA.seedReveal, i.e.A.seedReveal == H(B.seedReveal), thenB.rewardis not modified. - If
B.seedRevealis not a preimage ofA.seedReveal, i.e.A.seedReveal != H(B.seedReveal), thenB.rewardmust be equal to 0.
Also,
- if the forger of
Bdid not forge any block in the previous round or previously in the same round ofB,B.seedRevealcan be any value andB.rewardis not modified.
We assume that the delegate forging the block adjusts the reward property in the block in the case of the second bullet point. Note that in any other case (i.e., B.reward > 0 but B.seedReveal does not fulfil the rule in the first bullet point), B is invalid.
For this validation, only the properties generatorPublicKey, seedReveal and height for each block in the current and previous rounds are needed which may be kept in memory for efficiency reasons. LIP-0014 specifies that the block headers of the last three rounds are stored in memory, which will imply the availability of the required information if that proposal is already implemented.
Note that every value of seedReveal for a new forged block by each delegate reveals a new layer of the hash onion introduced before. In the Appendix B, an efficient way to compute and manage this hash onion for the delegates is proposed.
Random Seeds Computation
Once the first 51 blocks of the current round, round, have been forged, the two random seeds associated to round and used as input for the selection algorithm and the delegate list ordering for round + 1 can be computed. If round started at block height h, the first random seed, randomSeed1, is the output of the XOR of the valid seedReveal values contained in the blocks from height h - 51 to h + 51 and H(h + 51). The second random seed, randomSeed2, is the output of the XOR of the valid seedReveal values contained in the blocks from height h - 103 to h -1 and H(h - 1). Here XOR stands for the XOR bitwise operation.
For a specific B.seedReveal value in a block B with heightB.height between h - 103 and h + 51, when any of these two cases occur, B.seedReveal value is not valid and hence it is not input of the random seed computation:
- If the forger of
Bdid neither forge a block in the previous round nor previously in the same round ofB. - If
B.seedRevealis not a preimage ofA.seedReveal, i.e.A.seedReveal != H(B.seedReveal), whereAis the last block forged by the forger ofBin the previous round or the same round asB.
As in the previous subsection, the random seed computation can be performed efficiently if the block headers of the current round and the previous two rounds are stored in memory.
Weighted Random Selection Algorithm
The input parameters for the selection algorithm are:
- Assuming the current round,
round, an array with the set of standby delegates,ListStandbyDelegates, containing every delegate with rank > 101 and delegate weight ≥ 1000 LSK at the end of roundround- 2 is generated2. Each standby delegate object in the array has:- the public key of the delegate,
publicKey, - the delegate weight,
delegateWeight.
- the public key of the delegate,
- The random seeds
randomSeed1andrandomSeed2associated toroundand generated as per the specification in the previous subsection.
The output is the two selected standby delegates, delegate1 and delegate2 to be included in round+ 1.
Internally, the algorithm works as follows:
-
Sort
ListStandbyDelegatesin lexicographic order according to the combined key(delegateWeight, publicKey). -
Compute the sum,
WeightStandbyDelegates, of all the delegate weights inListStandbyDelegates. -
Compute
rnd1 = randomSeed1 mod WeightStandbyDelegates. -
Select first standby delegate
delegate1as:for i in {0,1,..., ListStandbyDelegates.length-1}: if (ListStandbyDelegates[i].delegateWeight > rnd1) delegate1 = ListStandbyDelegates[i] break else rnd1 = rnd1 - ListStandbyDelegates[i].delegateWeight end end -
Remove
delegate1fromListStandbyDelegates, recalculateWeightStandbyDelegatesand compute the second random number asrnd2 = randomSeed2 mod WeightStandbyDelegates. -
Repeat step 4 with
rnd2instead ofrnd1to selectdelegate2and stop afterwards.
In the case that ListStandbyDelegates contains less than 2 elements, the delegates with rank 102 and 103 will be chosen as delegate1 and delegate2 respectively.
Round Computation and Delegate List Ordering
The round computation is performed in the same way as in the current implementation with the difference that delegate1 and delegate2, as defined in the previous section, are included in the forging delegate list of round + 1. This implies the following:
- The round length is now 103 block slots. Currently, this is defined by the constant
ACTIVE_DELEGATES. For clarity, this constant should be replaced for three constants defining the number of the top 101 delegates bydelegateWeight, the number of standby delegates, i.e., 2, and the lenght of the round (sum of the two previous constants). - The change in the length of the round affects the logic to check when a round is finished which is 103 block slots in total.
-
delegate1anddelegate2have to be included in the delegate list3 before it is re-ordered forround+ 1. Currently, the functiongetKeysSortByVotecomputes this list before being re-ordered.
Bear in mind that this proposal does not change any other point in the round processing once the list with the 103 forging delegates for the next round is computed.
Delegate List Ordering
This proposal also updates the proposed changes in LIP-0003. The variable seedSource, defined in the first bullet point of the Specification section in that document, is redefined as:
var seedSource = randomSeed1;
The remaining changes of LIP-0003 remain the same and stay valid.
BFT Consensus Rules for Standby Delegates
Assuming that LIP-0014 is already implemented, standby delegates are expected to generate, process and validate new blocks as defined in the specifications of that LIP, i.e. in the same way an active delegate does it.
In order to preserve the properties introduced in Theorem 4.4 in A lightweight BFT consensus protocol for blockchains, votes and precommits implied by standby delegates have to be ignored. This implies that the logic specified at Computing Prevotes and Precommits subsection has to be skipped if newBlockheader was produced by a standby delegate, i.e., only blocks produced by active delegates and with heightPrevious < height imply prevotes and precommits.
Backwards Compatibility
The changes will introduce a hard fork for the following reasons:
- The block headers will include the
seedRevealproperty, which implies that the block signatures and the block validation logic will be different from the previous version. - The way in which the delegate list is computed every round changes from the previous version. Moreover, the delegate list will have 103 elements now and thus, rounds will be 2 slots longer.
Finally, for the migration, assuming that this LIP becomes active at height h, which is the height of the first block of round r, the following applies:
- It is assumed that Vk = 0 for k < h, where Vk are the values defined in Rationale section above.
- Since block headers for k < h do not have the property
seedReveal, it is assumed for the commit-reveal process that forging delegates in r did not forge any block before r.
Note that this only affects the standby delegate selection process of r and r + 1, which is not more biasable than the normal situation.
Reference Implementation
TBD
Appendix
A. Study on the Number of Forged Blocks for Standby Delegates
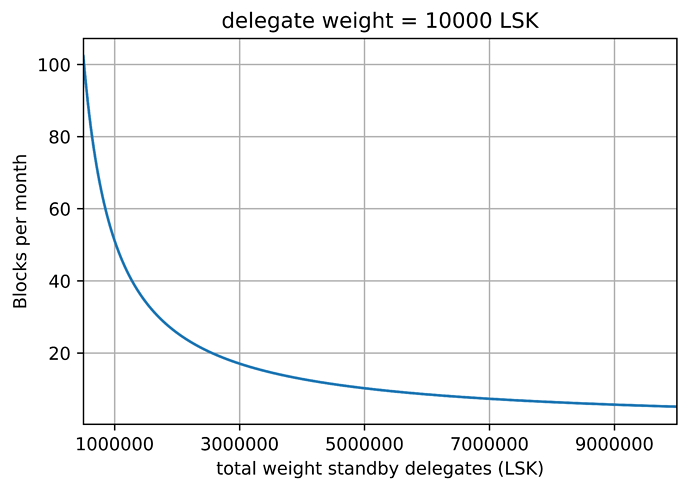
Assuming that a delegate gets a delegate weight of 10.000 LSK, which is enough to become a standby delegate, this appendix gives a basic estimation on the number of blocks this account is expected to forge in a certain period of time. The graph below provides this expectation in terms of average number of blocks per month against the total delegate weight of the standby delegates set.
It is worth mentioning that this study is assuming a uniform distribution of the weights in the standby delegate set where every delegate has a weight of 10.000 LSK. In practice, a standby delegate with this delegate weight may expect slightly higher figures, depending on the concrete delegate weight distribution.
B. Hash Onion Computation
Delegates should take good care of their own committed and revealed values so that they do not lose rewards unintentionally. In this appendix we describe a way for the delegates to locally compute and manage the hash onion with the values to be committed and revealed:
- Let S be a 16 bytes number generated by a cryptographically secure pseudo-random number generator. Then S is the initial input of the hash onion, H(H(H(… S…))), where H( ) is the hash function defined in Rationale section.
- Compute 1M hashes to generate the hash onion as
- h0 = S,
- hn = H( hn - 1) for n = 1,…,106.
- Store an ordered list with the last 1000 hashes as h106, …, h106-103.
- Store a second ordered list with the hash checkpoints every 1000 hashes until the initial preimage S as h106-103, …, h106-2*103, …, S.
- Start forging blocks revealing the entries of the list of step 3 in order.
- When the list at step 3 reaches the last entry, compute the next 1000 hash outputs starting from the next checkpoint, and store them in reversed order.
- Continue revealing the entries of the new list as in step 5.
- Repeat step 6 until the list at step 4 reaches the last entry.
With a hash onion of 1M layers as the one just described an active delegate can reveal a correct value for approximately 1M rounds, which is more than 30 years. There is a realistic chance that the delegate will miss a block (for unrelated reasons) before it runs out of preimages in the hash onion. Also, once a delegate misses a block, it is recommendable to compute a new hash onion to have a fresh start in the next forging opportunity.
Note that this is just a recommendation, and delegates can choose different parameters to generate their hash onion or any other process they may consider more suitable.
Notes
[1]: This is in line with LIP-0014, where a delay of 2 rounds is introduced to compute a new set of delegates.
[2]: For efficiency, this array can be computed at the end of round - 2 and kept in memory until the end of round. Another more general approach can be to store a snapshot of the delegateWeight values for the registered delegates at the end of round - 2 to be used for the algorithm and other potential purposes until the end of round.
[3]: This list is generated with a delay of 2 rounds as specified in Change of Delegates subsection of LIP-0014.